GPX' secrets
Nous examinons ici comment on peut exploiter les données contenues dans un fichier GPX à des fins de calculs statistiques. Notons que cette page d'information s'adresse à ceux qui sont intéressés par le codage... Les fichiers GPX sont produits par des dispositifs GPS (dédiés, genre Garmin) ou des Smartphones, tous équipés maintenant d'une puce GPS et de logiciels divers et variés pour l'enregistrement et le suivi de traces GPX. On sait aussi convertir des traces produites dans d'autres format (KML par exemple) en format GPX. Le présent texte ne s'intéresse qu'à la norme GPX.
1. Structure d'un fichier GPX
C'est un fichier texte à la norme XML, parfaitement éditable avec n'importe quel éditeur de texte. XML est un langage de balisage générique (semblable au HTML) qui permet de structurer librement des données afin qu'elles soient lisibles aussi bien par les humains que par des programmes de toutes sortes. Dans l'exemple ci-dessous, on comprend que la balise trk correspond à un tronçon, trkseg à un segment et trkpt à un point du segment. On voit que trkpt embarque la latitude et la longitude du point, que la balise ele correspond à l'altitude du point et que time spécifie l'horodatage du point. Les autres balise : gpx (obligatoire) et metadata (non obligatoire) contiennent des données variables en fonction du GPS (et du logiciel associé) qui a enregistré la trace GPX. Quant à la première ligne <?xml, elle indique qu'il s'agit d'un fichier XML. Comme pour le HTML, une balise s'ouvre et se ferme : <trkseg> ... </trkseg> ; on constitue ainsi un fichier clairement structuré et exploitable par la classe PHP simplexml facile à utiliser.
<?xml version="1.0" ...>
<gpx ...>
<metadata>
</metadata>
<trk>
<trkseg>
<trkpt lat="44.4599805" lon="4.1947116">
<ele>286.73</ele>
<time>2016-03-29T11:54:16Z</time>
</trkpt>
<trkpt lat="44.4598080" lon="4.1948168">
<ele>278.72</ele>
<time>2016-03-29T11:56:52Z</time>
</trkpt>
...
</trkseg>
<trkseg>
<trkpt lat="44.4599805" lon="4.1947116">
<ele>286.73</ele>
<time>2016-03-29T11:54:16Z</time>
</trkpt>
<trkpt lat="44.4598080" lon="4.1948168">
<ele>278.72</ele>
<time>2016-03-29T11:56:52Z</time>
</trkpt>
...
</trkseg>
...
</trk>
</gpx>
Noter qu'une trace trk peut contenir plusieurs segments trkseg ; c'est le cas lorsque l'on arrête le GPS (par exemple lors de la pause pique-nique de midi), puis qu'on le redémarre en précisant que l'on poursuit la même trace.
Séquence de code (extrait) pour le chargement et la récupération des données d'un fichier GPX :
<?php
$gpx = 'https://halbox.mimetik.org/VISUGPX/UPs/' . $_POST['nTrace' ] ; // on récupère l'adresse du fichier GPX téléchargé
$GPX = simplexml_load_file($gpx); // on charge le fichier GPX
$nbseg = count($GPX->trk->trkseg); // nombre de segments
$iseg = 0;
$ix =0;
while ($iseg < $nbseg) { // itération sur les segments de la trace
foreach($GPX->trk->trkseg[$iseg]->trkpt as $trkpt) { // itération sur les points d'un segment
$LATITUDE[$ix] = $trkpt['lat'];
$LONGITUDE[$ix] = $trkpt['lon'];
$ALTITUDE[$ix] = $trkpt->ele ;
$ix++;
}
$iseg++;
}
?>
L'exécution de ce code délivre dans 3 tableaux les coordonnées { latitude longitude altitude } de chaque point de la trace (d'où l'on tirera la distance et le dénivelé). Nous disposons donc de toutes les informations permettant le calcul de quelques statistiques utiles, telle que la distance, le dénivelé, la durée, etc... Et c'est ce que nous allons examiner maintenant.
2. Calcul de la distance
Nous n'utilisons pas les règles de la géométrie euclidienne mais celles de la géométrie sphérique, avec la formule Haversine permettant de calculer la distance entre 2 points situés sur une sphère (la Terre), points dont on connait les coordonnées géographiques {latitude longitude} :
Soit en langage PHP le code suivant :
<?php
class haversine {
function DistanceHaversine($latitude1, $longitude1, $latitude2, $longitude2) {
$r = 6371; // rayon moyen de la Terre
$lat1 = deg2rad($latitude1); // on convertit les degrés décimaux (norme GPX) en radians
$lat2 = deg2rad($latitude2);
$lon1 = deg2rad($longitude1);
$lon2 = deg2rad($longitude2);
$dp= asin(sqrt(pow(sin(($lat2-$lat1)/2),2)+cos($lat1)*cos($lat2)* pow(sin(($lon2-$lon1)/2),2)));
$dpr = 2*$dp*$r;
return $dpr;
}
}
?>
L'algorithme de calcul de la distance est donc simple dès lors qu'on sait calculer le distance entre 2 points : on calcule la distance entre le 1er et le 2iéme point, puis entre le 2ième et le 3ème point... jusqu'au deux derniers points, et on additionne le tout.
On peut aussi se baser sur la géométrie euclidienne avec le théorème de Pythagore a2 + b2 = c2, à partir du moment où on dispose des coordonnées UTM de nos 2 points : Y correspond alors à la position Nord/Sud par rapport à l'équateur (ordonnée en mètres), X à la position Est/Ouest d'une zone UTM (abscisse en mètres) - voir Wikidédia pour des explications détaillées. Le programme PHP ll2utm assure la conversion selon une formule relativement complexe (non explicitée ici), puis Pythagore est utilisé pour la calcul de la distance entre 2 points :
<?php
function ll2utm($lat,$lon) { // conversion coordonnées GEO {Lat Lon} vers UTM {X Y}
...
return $LatLon;
}
function DistancePythagore($latitude1, $longitude1, $latitude2, $longitude2) {
$LatLon1 = ll2utm(floatval($latitude1),floatval($longitude1));
$LatLon2 = ll2utm(floatval($latitude2),floatval($longitude2));
$x1 = pow(($LatLon2['lat'] - $LatLon1['lat']),2);
$x2 = pow(($LatLon2['lon'] - $LatLon1['lon']),2);
$dist = sqrt($x1 + $x2) / 1000; // m -> km
return $dist ;
}
?>
Le résultat est très proche de la distance Haversine, ce qui ne peut être étonnant s'agissant des petites distances d'un tracé de randonnée pédestre. Pour les diverses conversions possibles et la visualisation des zones UTM, cliquer sur le bouton de droite = conversion GEO {Lat,Lon} -> DMS (° ' '') et UTM {X,Y}
3. Calcul du dénivelé
On ne calcule pas le dénivelé, comme on le fait pour la distance, entre 2 points successifs puis sommation finale, car ce calcul est trop aléatoire. Prenons ce cas : un fichier GPX avec un très grand nombre de points. Si l'on calcule le dénivelé entre 2 points successifs, on peut trouver 0, puis encore 0 entre les 2 points suivants, etc... et au final on risque de trouver 0 pour un dénivelé réel pouvant être important. D'où l'idée de fixer un seuil de prise en compte du dénivelé entre 2 points (pas obligatoirement consécutifs) à 10 mètres, ce qui permet aussi de minimiser les erreurs de mesure des satellites. D'où cet algorithme :
- point n°1 de la trace GPX (c'est le point de départ) = point de référence ;
- on oublie les points suivants de la trace tant que l'écart entre le point courant et le point de référence est inférieur à 10 m;
- si un point est pris en compte dans le calcul, alors il devient le nouveau point de référence, etc... jusqu'au dernier point.
On fait la même chose pour le dénivelé négatif avec un seuil fixé à -10 mètres, et au terme du calcul itératif on obtient une "estimation" du dénivelé positif cumulé et du dénivelé négatif cumulé.
D'où cette séquence de code où on assume que $ALTITUDE est le tableau qui contient l'altitude de chaque point de la trace GPX et $ixm est le nombre total de points :
<?php
function denivele($altitude1,$altitude2) {
$a1 = floatval($altitude1);
$a2 = floatval($altitude2);
$ecart = $a2 - $a1;
return $ecart;
}
$deniv = 0;
$dpositif = 0;
$dnegatif = 0;
$ptref =$ALTITUDE[0]; // 1er point de référence = 1er point de la trace
$ix = 1;
while ($ix < $ixm) {
$alt = $ALTITUDE[$ix];
$deniv = denivele($ptref,$alt); // ecart entre les 2 points
if ($deniv >= 10) { // seuil fixé à 10 m
$dpositif = $dpositif + $deniv;
$ptref = $ALTITUDE[$ix];
}
if ($deniv <= -10) {
$dnegatif = $dnegatif +abs($deniv);
$ptref = $ALTITUDE[$ix];
}
$ix = $ix + 1;
}
?>
4. Calcul de la durée
L'horodatage pour chaque point d'une trace GPX est associé à la balise time et se présente sous cette forme : 2016-10-28T12:11:45Z (date du jour aaaa-mm-jj suivie de l'heure hh:mm:ss avec les caractères séparateurs T et Z). Pour connaître la durée du parcours, il suffit d'enregister l'horodatage du 1er et du dernier point de la trace, et de faire la différence, ce qui nécessite quelques calculs basiques au niveau de la chaîne de caractère horodatage.
Le temps de pause n'est pas encore calculé ; on peut penser à un algorithme capable de déceler le non-mouvement par le non-changement des coordonnées {latitude longitude} d'une série de points consécutifs ; de cette sélection d'une partie du fichier GPX, on pourra tirer le temps de pause en considérant les horodatages de début et de fin de la sélection. Par cumul des temps de pause de ces parties, on obtiendra le temps de pause total. Code à écrire...
5. Calcul du temps de pause
Calcul non réalisé...
6. Graphique du profil
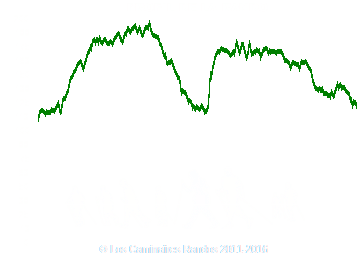
On utilise le programme PHP ykcee, via une interface permettant de spécifier tous les éléments constitutifs de la forme d'édition souhaitée. Extrait de notre spécification, incluse dans le programme graphix.php appelé par clic sur le bouton vert afficher les stats :
<?php
session_start();
include("YKCEE/ykcee.php");
$graph = new ykcee;
$graph->SetImageSize(360, 320);
$graph->SetFileFormat("png");
$graph->SetBackgroundColor("graphix");
$graph->SetChartBackgroundColor("graphix");
$graph->SetMaxStringSize(9);
$graph->SetChartBorderColor("graphix");
$graph->SetChartType("lines");
$graph->SetChartTitleSize(8);
$graph->SetChartTitle("PROFIL DE LA RANDO");
$graph->SetChartTitleColor("white");
$graph->SetBarColor(array("green")); // profil : couleur du tracé
$graph->SetLineThickness(5); // profil : épaisseur du tracé
$graph->SetAxisFontSize(7); // altitude en m
$graph->SetAxisColor("white");
$graph->SetTickLength(2);
$graph->SetTickInterval(16);
$graph->SetGridX(6);
$graph->SetGridY(0);
$graph->SetGridColor("white");
$graph->SetPointShape("dots");
$graph->SetShading(0);
$graph->SetNoData("Désolé... Y'a pas de données !");
...
$gpx = 'http://halbox.mimetik.org/VISUGPX/UPs/' . $_SESSION['latrace' ] ; // on charge la trace GPX
$GPX = simplexml_load_file($gpx);
$ix =0;
foreach($GPX->trk->trkseg->trkpt as $trkpt) { // récupération des altitudes $a (ordonnées du graphe à tracer) pour chaque point $ix (abscisses)
$a = (int)$trkpt->ele ;
$data[$ix] = array($ix, $a);
$ix++;
}
$graph->SetDataValues($data);
$graph->DrawGraph();
?>